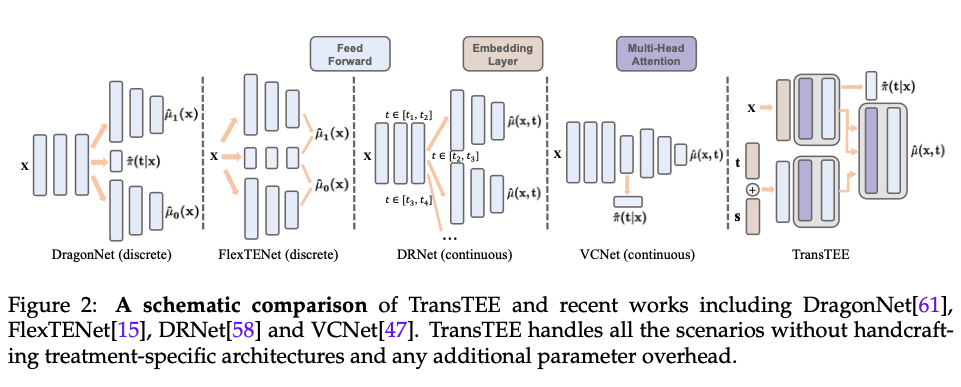
TransTEE

The paper introduced how to leverage the Transformer structure for the treatment effect estimation (TransTEE). Generally, the transformer’s input is a sequence of vectors, and therefore it is not straight forward to apply it to treatment effect estimation scenario which only has one feature vector per user. In the paper, the concept of sequence comes from two places

• Obtain an embedding for each feature (covariate) and therefore an input feature vector for a user with size \(R^{p}\) could be converted to a matrix \(R^{d*p}\) where \(d\) is the embedding dimension.
• For each treatment we also have an embedding. In this case when two treatments are applied to the user and we want to estimate the treatment effects, we would also obtain a sequence of vectors for the treatment

The below figure shows the structure of TransTEE. We concatenate the treatment and the dosage embedding and use MLP obtain the representation. Note here that the dosage input is not required while the paper uses the setup of continuous treatment in the medical field, and therefore it also uses dosage as an optional input. If multiple treatments are applied simultaneously, these treatments would be passed through series of self-attention to get the final representation for the treatments. On the other hand, for the input user features \(x\), it is passed through the embedding layer and the self-attention modules to capture the interaction between each feature dimension and obtain the final representation of each feature dimension. Finally, these feature representation would be treated as the memory (i.e. key and values for attention) in the Transformer decoder structure and the treatment representation would be treated as the query.

In this way with the Transformer decoder structure we could get the final representations and use an output layer to convert them to a continuous output. Need to note that if we applied multiple treatments simultaneously, we would have more than one representation before the output layer. In the paper it used pooling to merge these representations and do the treatment effects prediction.

Covariate embedding

The idea of covariate embedding allows us to capture the relation between each covariate by prepare the embedding for each covariate. In this way, with an input feature with dimension \(p\) we could have a sequence of covariate embedding with size \(d\).

The covariate embedding is implemented with one layer of MLP. The below is the code snippet from the author’s code.

    def __init__(self, **kwargs):
        # ...
        self.treat_weight = nn.Linear(1, emb_size)
        
        # ...
    
    def forward(self, x):
        # x is [batch, p]
        # ...
        ebd = self.treat_weight(x.unsqueeze(-1).to(torch.float32))  # x.unsqueeze(-1) make x to be [batch, p, 1]
        
        # ebd now is [batch, p, 1] x [1, d] = [batch, p, d]
        # ...

Propensity score modeling (Treatment modeling)

In paper’s section 4 it did not put too much context on how the propensity score modeling was implemented which was important since it’s using observational data. As a note here the paper is focusing on the continuous treatment, and therefore it’s not the exactly same concept of propensity score which is commonly used in the discrete treatment setup.

From the author’s implementation we could see that the continuous treatment is modeled with the mean pooling of covariate embedding over the \(p\) dimension.

    def forward(self, x):
        hidden = self.feature_weight(self.linear1(x))  # hidden: [batch, p, d]
        # ...
        
        return torch.mean(hidden, dim=1).squeeze(), Q  # The first returned tensor would be used in treatment modeling with size [batch, d]

Implementation

In addition to the author’s implementation, another implementation reference could be found in here.