Dragon Net

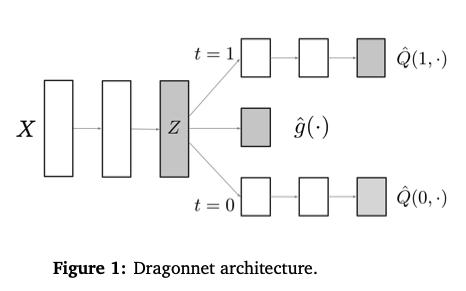
Dragon net is the model combining the uplift modeling and deep learning. It is proposed in this paper. In the paper, it used binary treatment as the example. The model structure is as the below figure. The input X is feed into layers of neurons which is the feature extraction process. Once the feature representation Z is extracted, there are three heads following. One head is generating the propensity score (\(\hat{e}\)) which is predicting the probability of the input receives treatment. The other two heads (\(\hat{f}_1\) and \(\hat{f}_0\)) are predicting the outcome of receiving the treatment and not receiving the treatment.

Intuitively, the loss would be the following

\[\sum_{i} [y_i - \hat{f}_{T_i}(x_i)]^2 + \lambda Xent(T_i, \hat{e}(x_i))\]

However, the \(\hat{f}_{T_i}\) estimator above would suffer from the confounding bias since the loss does not consider the interaction between the uplift and the propensity score.

Targeted Regularization

The author used the section 3 to illustrate the idea of targeted regularization. The loss function is the below

\[\textrm{T-Loss} = \{y_i - [\hat{f}_{T_i}(x_i) + \epsilon (\frac{T_i}{\hat{e}(x_i)} - \frac{1-T_i}{1 - \hat{e}(x_i)}) ] \}^2\]

and the final loss function for instance \(i\) is now

\[[y_i - \hat{f}_{T_i}(x_i)]^2 + \lambda Xent(T_i, \hat{e}(x_i)) + \beta \textrm{T-Loss}\]

During inference, we are using the following to estimate CATE

\[\textrm{CATE} = \tilde{f}_{1}(x) - \tilde{f}_0(x)\] \[\tilde{f}_t(x) = \hat{f}_t(x) + \epsilon (\frac{t}{\hat{e}(x)} - \frac{1-t}{1 - \hat{e}(x)})\]

In the paper it states that if we are minimizing the above final loss function, the CATE estimator would satisfy the equation 3.1 and therefore the CATE estimator would converge to the true estimator at a fast rate and is asymptotically the most data efficient estimator possible.

By observing the targeted regularization, we could see that it is similar to the doubly robust (DR) estimator which is

\[\textrm{CATE}_{DR}(x_i) = \hat{f}_1(x_i) - \hat{f}_0(x_i) + (y_i - \hat{f}_{T_i}(x_i))(\frac{T_i}{\hat{e}(x_i)} - \frac{1-T_i}{1 - \hat{e}(x_i)})\]

They all follow the form of \(\textrm{initial CATE estimation} + (\textrm{correction term}) * (\textrm{propoensity weighting})\)

while in the DR estimator the correction term is obtained through labels and here in the dragon net the correction is a learnable parameter.

Implementation

An implementation reference could be found here.