The article is based on the following source:

• The Evolution of Multi-task Learning Based Video Recommender Systems - Part 1
• Mixture-of-Experts based Recommender Systems
• Mixture of Experts Explained

Why multi-task learning (MTL)

Nowadays, an industry-level recommendation system (RecSys) often uses a MLT model for their ranking.

• Requirement for multiple objectives: For example, a video recommendation system would need to balance the click-through-rate (CTR), video watch completion rate, user watch time, user retention…etc.
• Better model performance: Among the objectives, Some of them are correlated while some are conflicted. MLT learns relevant information from different objectives and theoretically could give us a model that are more generalized.
• Better serving efficiency: For serving different tasks, a MTL model could save a lot of computations since many parameters are shared

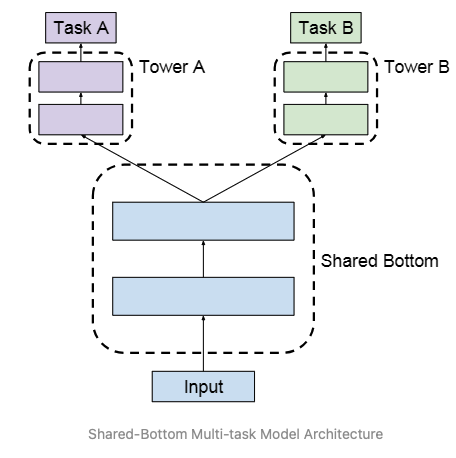
Shared-bottom MTL

• The simplest structure
• The bottom learned the features that are shared across all tasks and the task specific information is learned in the task towers
• Sensitive to relationships among tasks
  • Weak or complex relations between tasks would lead to performance degradation (negative transfer)
    • The structure design (inductive bias) of shared bottom is conflicted with the fact that the tasks are unrelated or even conflicted
• More on negative transfer
  • MTL results in worse performance on some/all tasks when these tasks are trained individually
    • Knowledge obtained from other tasks is useless/harmful
  • Potential causes
    • Conflicting Gradients
    • Gradient Magnitude Differences
    • Imbalanced Loss Scales
    • Task Conflicts
    • Knowledge Interference
• Seesaw effect issue
  • Improve one task and hurt others

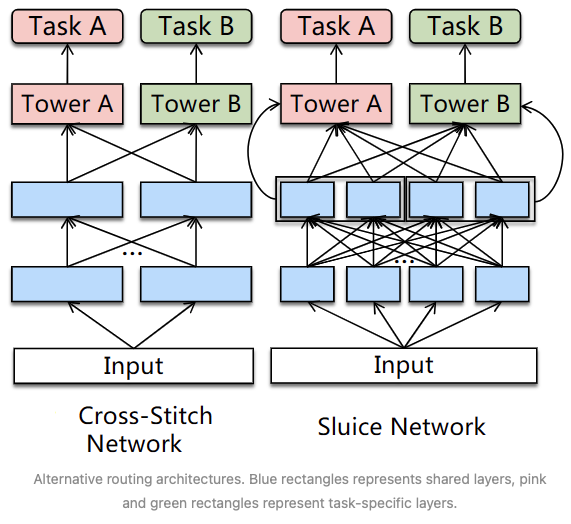
A simple way to combat the conflicted targets is to separate the whole shared encoder into several encoders, and attach linear combination layers to allow flexible parameter sharing (see the graph below.) In other words, if the tasks are conflicted and the optimal choice is not to share parameters at all, the linear combination weights would become a one-hot vector.

However, people find the improvements are very limited.

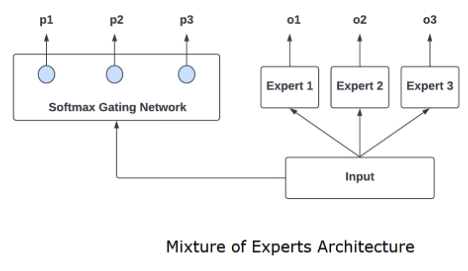
Gating structure

Instead of adding complex linear combination layers, here we structure the model in a more straightforward design.

• The model is now composed with multiple experts
• Each expert learn an aspect of the input data
• When we are doing the inference, we have a gating network to fuse these experts’ prediction together
• The design is called mixture of experts (MoE)

Why gating structure

Intuitively speaking, it seems that the gating structure of MoE is just another way of learning linear combination. However, in reality there is a difference.

• With the naive way of linear combination, each expert would need to learn the residual errors from other experts, and the dynamics make the learning harder
• In contrast, the gating structure would decide which expert to use and effectively make each expert’s learning independent

To show how the gating structure learns how to decide the experts, consider the MSE optimization case below.

• MSE loss \(L = (y-\sum_i p_i * o_i)^2\). \(p_i\) is the gating output on expert \(i\), \(o_i\) is the expert \(i\)’s output
• For the derivative of gating output \(p_j\), we have \(\frac{\partial L}{\partial p_j} = (y - \hat{y}) * (-1) * o_j\) where \(\hat{y} = \sum_i p_i * o_i)\)

We could interpret \((y - \hat{y}) * (-1) * o_j\) as the follow

• If \((y - \hat{y}) < 0\), it means the model’s overall prediction is underestimating
• In this case, the gating network would be pushed to give the experts whose output is larger to have more weights to boost the overall estimating

Comparing linear combination and the gating network

• In linear combination, \(p_i\) is static and the same across all inputs
• In the gating network, \(p_i\) is parameterized and different for different input
• In linear combination, we always use the same combination for all inputs while in the gating network the network choose the experts to handle the input

The above difference is why the gating network could resolve the coupling issue of linear combination.

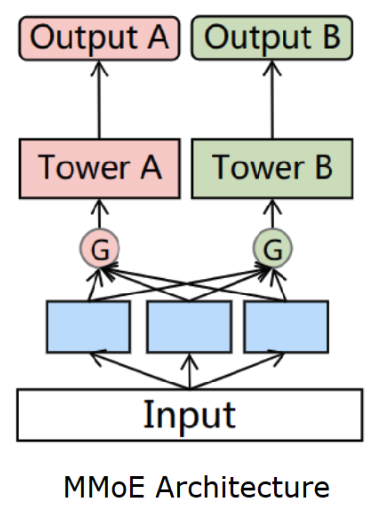
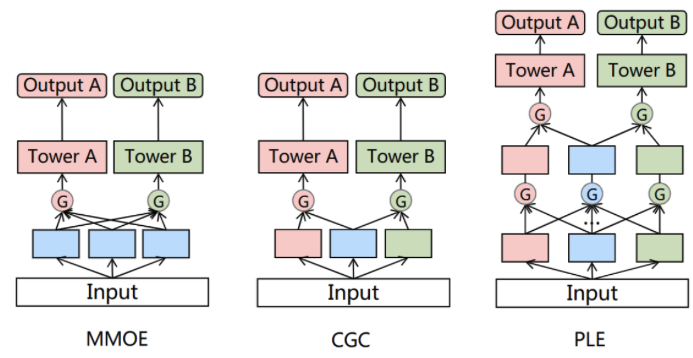
On top of the MoE, MMoE extends the structure to support multi-task learning.

• If we have two tasks, there would be two gating networks to learn the task specific gating
• Each task has their own task-specific tower after receive the outputs from the gating network
• Google reported significant gains from the structure for the YouTube recommendation [paper]

Tencent proposed more advanced versions of MMoE.

Customized Gate Control (CGC)

• New idea of having task-specific experts
• The task-specific knowledge only feed into the corresponding tasks’ gates
• Each gate output the combination of shared experts and the task experts
• Mitigate the seesaw phenomenon

Progressive Layered Extraction (PLE)

• Stacking multiple CGC layers

An example implementation notebook could be found here